Inversions

One interesting way to think about chords is to view them not as their name (like “major”, “minor”, “diminished”, or “dominant 7th”), but simply as a group of notes. Any group of pitches can make a chord, there might not be a name for it like “augmented”, but there are ways of notating those chords. Some people use numbers where either 0 or 1 is used for the first note, the “root” of the chords. And then numbers are assigned to each note ascending chromatically.

Using this notation a C major chord (C E G) would be written as 1 5 8 or 0 4 7.

This notation also often re-arranges notes to have the smallest intervals at the bottom of the chord. For example a C major 7 chord (C E G B) would be re-arranged to be written as B C E G, so that the half step between B and C is at the “bottom” of the chord. This chord would them be analyzed as 1 2 6 9 or 0 1 5 8.

If you’d like to learn more about this notation I suggest you read “Introduction to Post-Tonal Theory” by Joseph Straus.

One thing this notation and style of thinking lets you do is invert chords in a way that’s different than standard chord inversions.

Inversions are normally thought of as changing the bass note of a chord. For example if a C major chord is played with an E note in the bass, or as the lowest pitched note, that is considered “first inversion.” If a G note is in the bass it is considered “second inversion.”

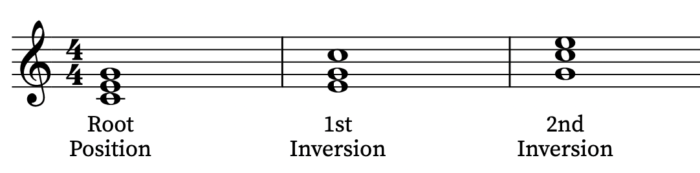
If we “invert” chords in this new way we are re-creating the chord with descending intervals, rather than ascending intervals.

For example we can take that first chord of 1 5 8, spelled as C E G, and “invert” it to get C Ab F. The way this works as an inversion, in this style of analysis, is because C up to E is the interval of a major third and C down to Ab is the same interval, a major 3rd. The interval from C up to G is a perfect 5th and the interval of C down to F is a perfect 5th as well.

This can create some interesting chords and harmonic progressions that still sound related because the structures are still the same in some respect, but they may be harmonic progressions you’d be less likely to come up with or use when thinking in terms of traditional functional harmony.

Let’s look at another example.

A major 7th chords spelled C E G B we’ll re-write as B C E G and use the number notation of 1 2 6 9. If we take these same intervals and spell the chord downwards we’d spell out B A# F# D#. Notice these two chord structures are the same chord quality. They’re both major 7th chords, just spelled out differently. If we spell that same chord downwards from C we’d get a C major 7th chord as well C B G E.

This can be a confusing notation and style of analyzing and thinking about music if you’ve never done it before, but give it a try and write a few pieces thinking about the music this way and it’ll become a whole lot easier.

ISJ